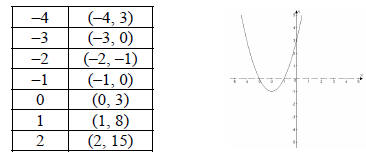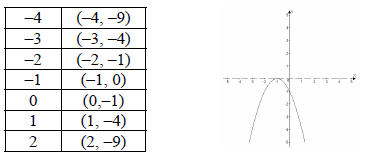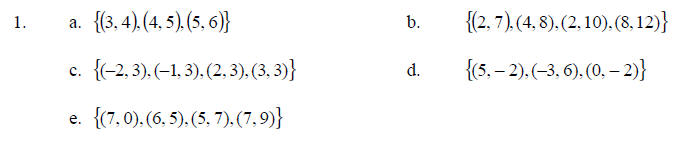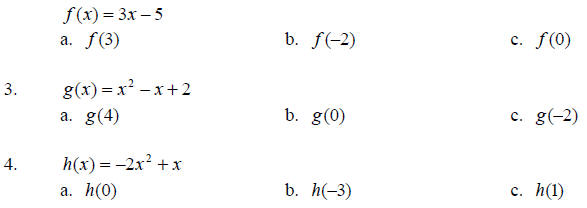Solving Quadratic Equations
Mini Lecture 10.1
Learning Objectives:
1. Solve quadratic equations using the square root property.
2. Solve problems using the Pythagorean Theorem.
3. Find the distance between two points.
Examples:
1. Solve each quadratic equation by the square root property. If possible,
simplify radicals
or rationalize denominators.
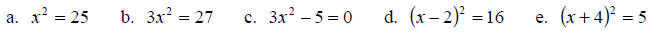
2. Solve each quadratic equation by first factoring the perfect square on the
left. Then apply
the square root property. Simplify radicals, if possible
a. x2 + 6x + 9 = 64
b. x2 + 8x +16 = 11
3. Use the Pythagorean Theorem to solve the following.
If a ladder is angled against a home and it is 6 ft. from the base of the
home and reaches 8
ft. high on the side of the home, how tall is the ladder?
4. Find the distance between the given 2 points. Express answers in simplest
radical form
and if necessary, round to two decimal places.
a. (– 3, 6)and (1, 5)
b. (5, – 3)and (9, −6)
Teaching Notes:
• If u2 = d is being in an algebraic expression and d is a positive real number,
then there
will be exactly two solutions: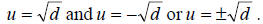
• The Pythagorean Theorem states that the sum of the squares of the lengths of
the legs of a
right triangle equals the square of the length of the hypotenuse. If the lengths
of the legs
are a and b, and the hypotenuse has length c, then
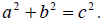
• The Distance Formula is used to find the distance between two points in the
rectangular
coordinate system
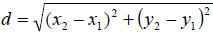 given 2 points
given 2 points
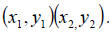
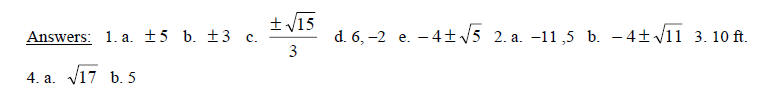
Mini Lecture 10.2
Solving Quadratic Equations by Completing the Square
Learning Objectives:
1. Complete the square of a binomial.
2. Solve quadratic equations by completing the square
Examples:
1. Complete the square for each binomial by adding “one-half the coefficient of
the x term
squared.” Then factor the resulting perfect square trinomial.
a. x2 + 2x + __________ = __________ b. x2 + 8x + __________ = __________
c. x2 – 16x + _________ = __________ d. x2 +10x + _________ = __________
e. x2 – 14x + _________ = __________ f. x2 + 3x + __________ = __________
g. x2 – 6x + __________ = __________
2. Solve each quadratic equation by completing the square
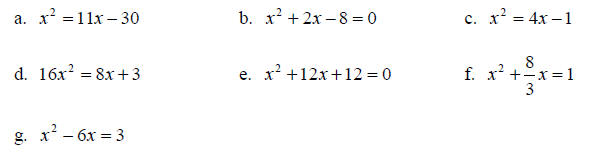
Teaching Notes:
• Remind students that in order to complete the square the leading coefficient
must be 1
and there must be an x2 term and an x term.
• When using completing the square to solve a quadratic equation, the variable
terms must
be on one side of the equation and the constant term on the other side before
starting the
process.
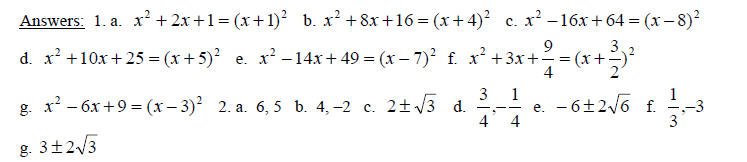
Mini Lecture 10.3
The Quadratic Formula
Learning Objectives:
1. Solve quadratic equations using the quadratic formula.
2. Determine the most efficient method to use when solving quadratic equations.
3. Solve problems using quadratic equations.
Examples:
1. Solve each equation using the quadratic formula.
a. 3x2 +10x + 3 = 0
b. x2 = 5x + 2
c. x2 + 3x = –1
2. Solve each equation by the method of your choice. Simplify irrational
solutions, if
possible.
a. 2x2 = 40
b. (x + 4)2 = 8
c. 3x2 – 4x +1 = 0
d. 2x2 + 7x + 4 = 0
e. 4x2 + 2x – 5 = 0
3. A football is kicked straight up from a height of 2 feet with an initial
speed of 50 ft. per
second. The formula h = –16t2 + 50t + 2describes the ball’s height above the
ground, h,
in feet, t seconds after it is kicked. Using your calculator, find when the ball
will hit the
ground. Round to the nearest tenth of a second.
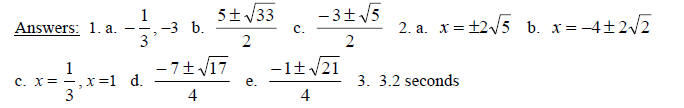
Mini Lecture 10.4
Imaginary Numbers as Solutions of Quadratic Equations
Learning Objectives:
1. Understand the concepts:
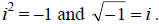
2. Express square roots of negative numbers in terms of i.
3. Solve quadratic equations with imaginary solutions.
Examples:
Write as a multiple of i.
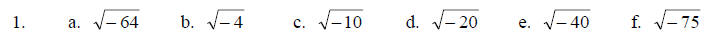
Solve each quadratic equation using the square root property.
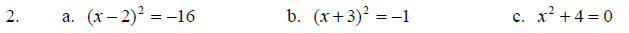
Solve each quadratic equation using the quadratic formula.
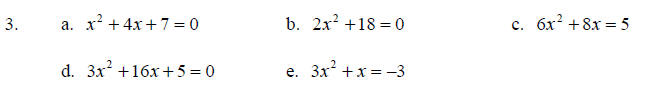
Teaching Notes:
• When simplifying the square root of –1, it is helpful to write the “i” to the
left of the
radical so it does not look like the “i” is under the radical.
• Always simplify the
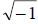 first.
first.
• Remind students that in order to use the square root property to solve a
quadratic
equation, there must be a perfect square containing the variable isolated on 1
side of the
equation.
• Students need to be cautioned again about watching the signs very carefully
when using
the quadratic formula.
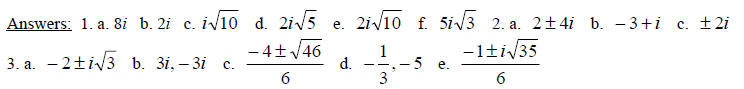
Mini Lecture 10.5
Graphs of Quadratic Equations
Learning Objectives:
1. Understand the characteristics of graphs of quadratic equations.
2. Find a parabola’s intercepts.
3. Find a parabola’s vertex.
4. Graph quadratic equations.
5. Solve problems using a parabola’s vertex.
Examples:
1. Consider the quadratic equation: y = x2 + 4x + 3.
a. Will the parabola open upward or downward?
b. Complete the table of values and graph the parabola.
| x |
y = x2 + 4x + 3 |
(x, y) |
| –4 |
|
|
| –3 |
|
|
| –2 |
|
|
| –1 |
|
|
| 0 |
|
|
| 1 |
|
|
| 2 |
|
|
c. Find the x-intercepts.
d. Find the y-intercepts.
e. Find the vertex.
2. Complete the same steps a, b, c, d, e, from number 1 for the equation: y =
–x2 – 2x –1.
Teaching Notes:
• The graph of quadratic equation y = ax2 + bx + c , a ≠ 0 is called a parabola.
If a is
positive, the parabola opens upward. If a is negative, the parabola opens
downward.
• The vertex, or turning point, of the parabola is referred to as the maximum if
the parabola
opens downward and the minimum if the parabola opens upward.
• Parabolas are symmetric with respect to a line known as the axis of symmetry
that runs
through the vertex. The two halves match exactly.
• To find the x-intercepts, let y = 0. Then factor or use the quadratic formula
to solve for x.
• To find the y-intercept, let x = 0 and solve for y.
• To find the vertex of a parabola with the equation, y = ax2 + bx + c , first
solve for x.
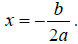 Then substitute the value of x into the parabola’s equation and evaluate.
Then substitute the value of x into the parabola’s equation and evaluate.
• After plotting the vertex and intercepts, make sure to connect with a smooth
curve.
Answers:
1. a. up
b.
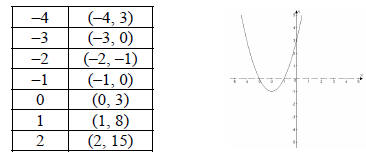
c. x-intercepts (–3, 0)(–1, 0)
d. y-intercept (0, 3)
e. vertex (–2 , –1)
2. a. down
b.
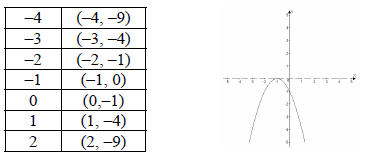
c. x-intercept (–1, 0)
d. y-intercept (0 , –1)
e. vertex (–1 , 0 )
Mini Lecture 10.6
Introduction to Functions
Learning Objectives:
1. Find the domain and range of a relation.
2. Determine whether a relation is a function.
3. Evaluate a function.
4. Use the vertical line test to identify functions.
Examples:
Determine whether relation is a function. Give the domain and range for each
relation.
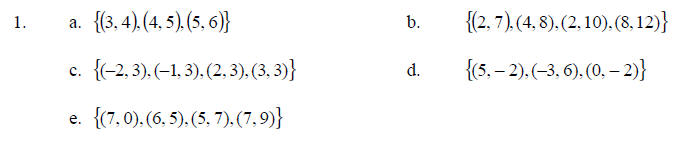
2. Evaluate the functions at the given values.
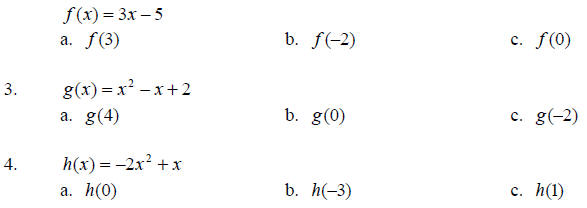
5. Use the vertical line test to identify graph in which y is a function of
x.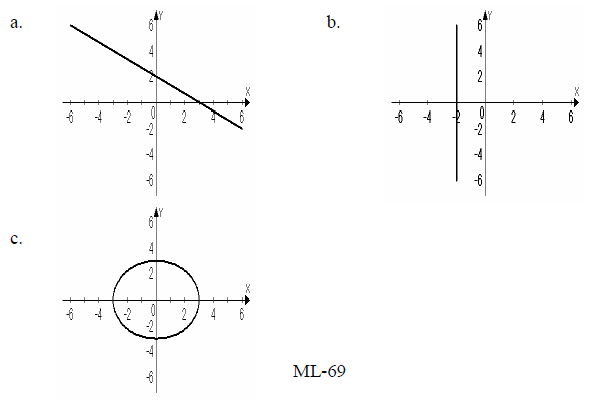
Teaching Notes:
• Students should understand that every function is a relation BUT not every
relation is a
function.
• The domain of a relation or a function is all the x-values or possible
x-values.
• The range of a relation or a function is all the y-values or possible
y-values.
• A function is a relation in which no two x values are the same.
• “f(x)” and “y” are like math synonyms.
• f(x) indicates a function.
Answers: 1. a. function; domain {3, 4, 5}; range {4, 5, 6}
b. not a function; domain {2, 4, 8}; range {7, 8, 10, 12}
c. function; domain {–2, –1, 2, 3}; range {3}
d. function; domain }5, –3, 0}; range {–2, 6}
e. not a function; domain {7, 6, 5}; range {0, 5, 7, 9}
2. a. f (x) − 6x + 7 b. f (x) = 2x2 + 5 3. a. 4 b. –11 c. –5 4. a. 14 b. 2 c. 8
5. a. 0
b. –21 c. –1 5. a. function b. not a function c. not a function
|


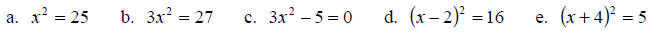
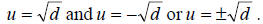
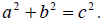
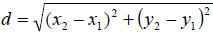 given 2 points
given 2 points
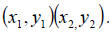
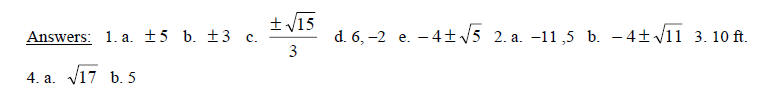
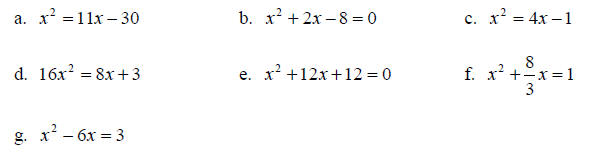
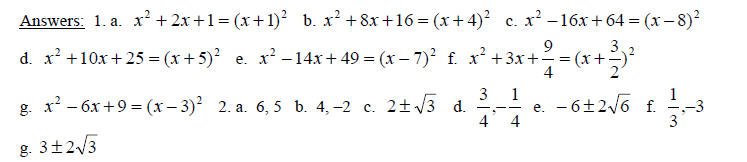
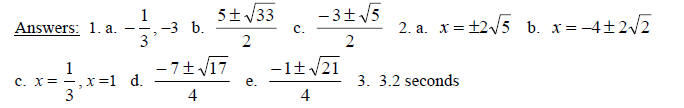
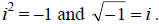
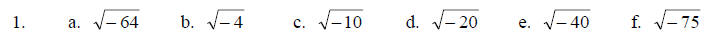
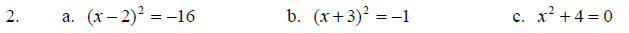
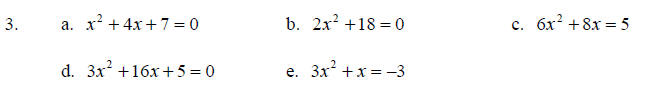
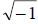 first.
first.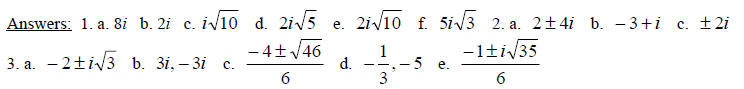
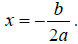 Then substitute the value of x into the parabola’s equation and evaluate.
Then substitute the value of x into the parabola’s equation and evaluate.