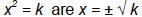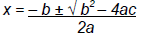|
Home Graphing and Writing Linear Functions SOLVING EQUATIONS INVOLVING RATIONAL EXPONENTS Linear Equations and Graphing Systems of Linear Equations Solving Polynomial Equations Matrix Equations and Solving Systems of Linear Equations Introduction Part II and Solving Equations Linear Algebra Graphing Linear Inequalities Using Augmented Matrices to Solve Systems of Linear Equations Solving Linear Inequalities Solution of the Equations Linear Equations Annotated Bibliography of Linear Algebra Books Write Linear Equations in Standard Form Graphing Linear Inequalities Introduction to Linear Algebra for Engineers Solving Quadratic Equations THE HISTORY OF SOLVING QUADRATIC EQUATIONS Systems of Linear Equations Review for First Order Differential Equations Systems of Nonlinear Equations & their solutions LINEAR LEAST SQUARES FIT MAPPING METHOD FOR INFORMATION RETRIEVAL FROM NATURAL LANGUAGE TEXTS Quadratic Equations Syllabus for Differential Equations and Linear Alg Linear Equations and Matrices Solving Linear Equations Slope-intercept form of the equation Linear Equations DETAILED SOLUTIONS AND CONCEPTS QUADRATIC EQUATIONS Linear Equation Problems Systems of Differential Equations Linear Algebra Syllabus Quadratic Equations and Problem Solving LinearEquations The Slope-Intercept Form of the Equation Final Exam for Matrices and Linear Equations Linear Equations |
Quadratic Equations and Problem SolvingQuadratic Equations and Problem Solving We now focus on solving quadratic equations. Recall we learned how to solve
for linear equations Note -> a quadratic equation can have zero, one, or two real solutions. Quadratic Equation: A quadratic equation in one variable is an
equation that can be written in the Solving Quadratic Equations 4 basic symbolic strategies: Factoring, Square Root Property, Completing the Square, Quadratic Formula Ex: x^2 - 4 = 0 Square Root Property -> Let k be a nonnegative number. Then the solutions to the equation
Ex: x^2 - 4 = 0 -> Completing the Square -> useful when solving quadratic equations that
do not factor easily! Quadratic Formula -> solutions to the quadratic equation ax^2 + bx + c = 0 , where a ≠ 0, are
Ex: Discriminant: In the quadratic formula, the quantity b^2 – 4ac is called the
discriminant. The Note -> When a quadratic equation is solved graphically, the parabola
intersects the x-axis 0, 1, • If b^2 – 4ac > 0, there are 2 real solutions GRAPHICALLY
NUMERICALLY
Problem Solving Exs: |