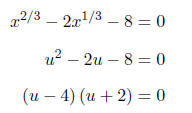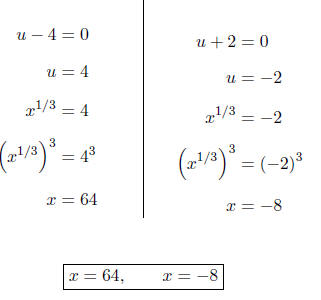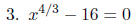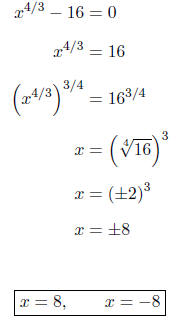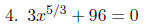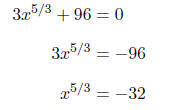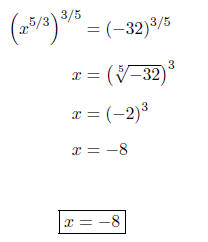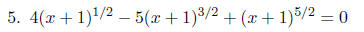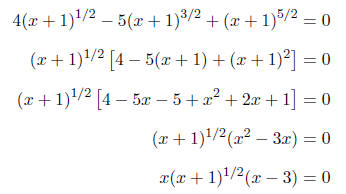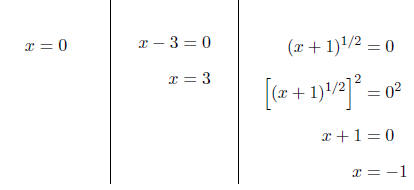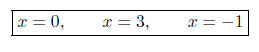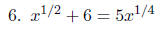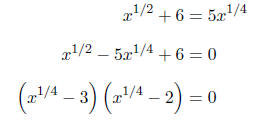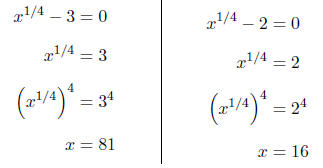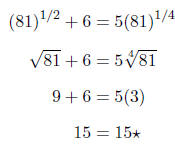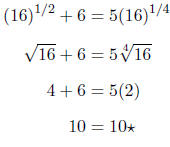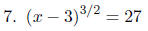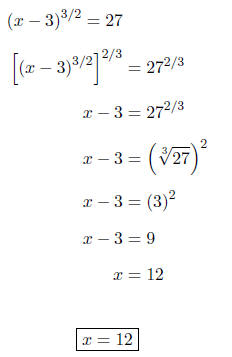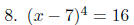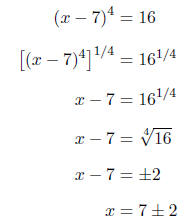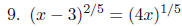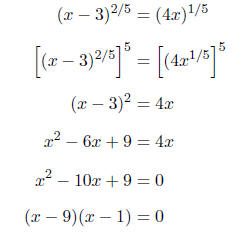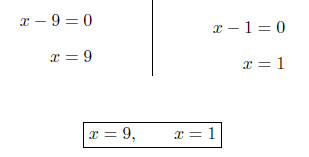|
Home Graphing and Writing Linear Functions SOLVING EQUATIONS INVOLVING RATIONAL EXPONENTS Linear Equations and Graphing Systems of Linear Equations Solving Polynomial Equations Matrix Equations and Solving Systems of Linear Equations Introduction Part II and Solving Equations Linear Algebra Graphing Linear Inequalities Using Augmented Matrices to Solve Systems of Linear Equations Solving Linear Inequalities Solution of the Equations Linear Equations Annotated Bibliography of Linear Algebra Books Write Linear Equations in Standard Form Graphing Linear Inequalities Introduction to Linear Algebra for Engineers Solving Quadratic Equations THE HISTORY OF SOLVING QUADRATIC EQUATIONS Systems of Linear Equations Review for First Order Differential Equations Systems of Nonlinear Equations & their solutions LINEAR LEAST SQUARES FIT MAPPING METHOD FOR INFORMATION RETRIEVAL FROM NATURAL LANGUAGE TEXTS Quadratic Equations Syllabus for Differential Equations and Linear Alg Linear Equations and Matrices Solving Linear Equations Slope-intercept form of the equation Linear Equations DETAILED SOLUTIONS AND CONCEPTS QUADRATIC EQUATIONS Linear Equation Problems Systems of Differential Equations Linear Algebra Syllabus Quadratic Equations and Problem Solving LinearEquations The Slope-Intercept Form of the Equation Final Exam for Matrices and Linear Equations Linear Equations |
SOLVING EQUATIONS INVOLVING RATIONAL EXPONENTSDefinition:
(If n is even then we require a ≥ 0.) In other words, in a
rational exponent, the numerator indicates
Important Properties: • To solve Common Mistakes to Avoid: • Although you can raise both sides of an equation to the
same power without changing the solutions, • Remember that whenever you have the even root of a
positive number, we get two answers: one • Do NOT attach a • Make sure that the variable is isolated before raising both sides to the same power. For example,
PROBLEMS Solve for x in each of the following equations.
First, we will isolate the variable.
Next, we will raise both sides to the 3/2
Notice that we are unable to isolate the vari-
Setting each factor equal to zero, we obtain
OR (for an alternative way)
Setting each factor equal to zero, we obtain
First, we will isolate the variable. Then we
First, we will isolate the variable.
Next, we will raise both sides to the 3/5
First, we will factor this expression com-
Setting each factor equal to zero, we obtain
If we check x = -1 by substituting back into
Since we cannot isolate the variable, we will
Setting each factor equal to zero, we get
Because we raised both sides to an even
Notice that the quantity containing the ra-
Notice that although this equation does not
Simplifying this last equation we get
Notice that we cannot solve this one by fac-
Setting each factor equal to zero, we obtain
|
||||


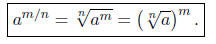
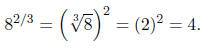
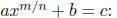 First,
isolate the variable. Then, raise both sides of the expression to the
First,
isolate the variable. Then, raise both sides of the expression to the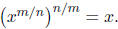 Finally,
solve for the variable.
Finally,
solve for the variable.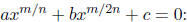 Try to factor and use the zero
product property.
Try to factor and use the zero
product property.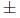 when
working with odd roots. When you take the odd root of a number, you
when
working with odd roots. When you take the odd root of a number, you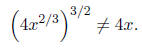
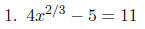
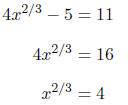
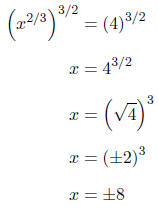

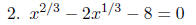
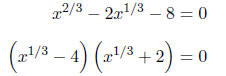
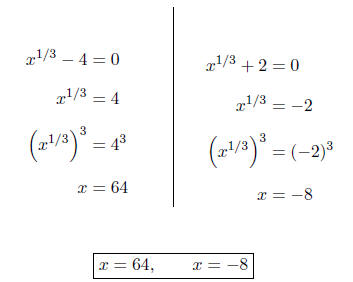
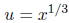 , we get
, we get