Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

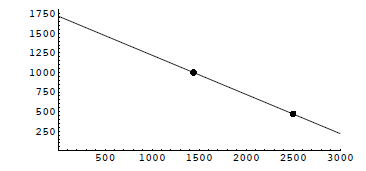
Linear Equations

• Price-Demand
• Price-Supply
• Simple Interest
• Linear equation practice problems

Price versus quantity demanded:
Several companies make a 37 inch, Plasma HDTV. Right now,
they sell for an average of $1440. But what if the price goes
up? Then consumer demand will decrease. But if the price goes
down, then consumer demand will increase. Consumer demand
depends on the price.

Symbols:

• Price: p is the selling price for the TV.
• Demand: d is the number of TVs (in thousands) sold.

The quantity d of TVs sold (demanded) is related to the price p
as follows:
d = 1720 − .50p

Can you see how the equation below reflects the relationship?

Price-demand equation: d = 1720 − .50p
We are interested in pairs of number d and p (written (d, p))
that satisfy this equation. Such a pair is called a solution to the
equation.

What is the demand (in thousands) if the price is $1440?
What is the demand if the price is $2500?
What price should we charge if we want to sell 500 thousand
TVs?

Price-demand equation: d = 1720 − .50p

The demand (in thousands) if the price is $1440 is
d = 1720 − (.50)(1440) = 1000 thousand TVs (one million)

What is the demand if the price is $1441?

The demand (in thousands) if the price is $2500 is
d = 1720 − (.50)(2500) = 470 thousand TVs

What is the demand if the price is $2501?
If price increases $1 how does demand change?

Price-demand equation: d = 1720 − .50p. Represent all such
solutions on a graph. Why is it straight?

What point above represents the situation where the price is
$1440?
What point above represents the situation where the price is
$2500?
What point above represents the situation where the demand is
500 thousand TVs?

Price-demand equation: d = 1720 − .50p.

What are some other ways to write this equation?
What would it tell us if we solved for p in terms of d?

The equation d = 1720−.50p is and example of a linear equation
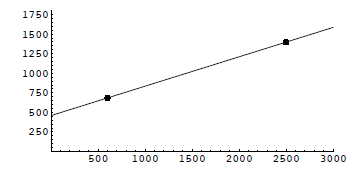
in two variables.

Price-supply:
The companies that make the 37 inch HDTVs are willing to
produce more TVs if they can sell them at a higher price. So
the supply of TVs is also related to the price at which these TVs
will sell.

The supply equation in this case is:
s = .375p+460
Again, supply is measured in thousands of TVs. This is also a
linear equation in two variables.

How does this equation match the description above?

Price-supply equation: s = .375p+460. Again we can represent
many solutions at once with a graph. Moreover we can use the
graph to answer questions about the equation.

What is the supply (in thousands) if the price is $600?
What is the supply if the price is $2500?

At what price does the quantity demanded match the quantity
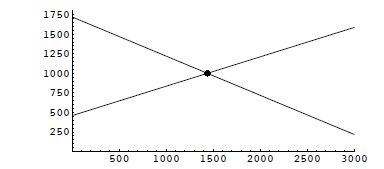
supplied?

Price-demand function: d = 1720 − .50p
Price-supply function: s = .375p+460

Solve d = s. What does this have to do with the price p? Did you
have a linear equation? In how many variables? Clicker question

Simple Interest Formula:
Consider the following Symbols

• Principal P
• Interest rate (annual) r
• Time t
• Amount of money at end of investment period.

These are also related by a linear equation: A = P +Prt.

Solve for r. What does this mean?
Solve for t. What does this mean?

More Practice:
[Matched problem 8 Section1.1] Mary paid 8.5% sales tax and a
$190 title and license fee when she bought a new car for a total
of $28,400. What is the purchase price of the car?

More Practice:
[Matched problem 9 Section1.1] How many CDs would a recording
company have to make and sell to break even if the fixed
costs are $18,000, variable costs are $5.20 per CD and the CDs
are sold to retailers for $7.60 each?