|
Home Graphing and Writing Linear Functions SOLVING EQUATIONS INVOLVING RATIONAL EXPONENTS Linear Equations and Graphing Systems of Linear Equations Solving Polynomial Equations Matrix Equations and Solving Systems of Linear Equations Introduction Part II and Solving Equations Linear Algebra Graphing Linear Inequalities Using Augmented Matrices to Solve Systems of Linear Equations Solving Linear Inequalities Solution of the Equations Linear Equations Annotated Bibliography of Linear Algebra Books Write Linear Equations in Standard Form Graphing Linear Inequalities Introduction to Linear Algebra for Engineers Solving Quadratic Equations THE HISTORY OF SOLVING QUADRATIC EQUATIONS Systems of Linear Equations Review for First Order Differential Equations Systems of Nonlinear Equations & their solutions LINEAR LEAST SQUARES FIT MAPPING METHOD FOR INFORMATION RETRIEVAL FROM NATURAL LANGUAGE TEXTS Quadratic Equations Syllabus for Differential Equations and Linear Alg Linear Equations and Matrices Solving Linear Equations Slope-intercept form of the equation Linear Equations DETAILED SOLUTIONS AND CONCEPTS QUADRATIC EQUATIONS Linear Equation Problems Systems of Differential Equations Linear Algebra Syllabus Quadratic Equations and Problem Solving LinearEquations The Slope-Intercept Form of the Equation Final Exam for Matrices and Linear Equations Linear Equations |
Solution of the EquationsFUNDAMENTAL THEOREM OF ALGEBRA Theorem. Suppose p(x) is any polynomial of degree n
> 0. Then there is at Explanation: Suppose
Let r be a large enough radius to make p(x) ≈ xn a good
approximation (whatever Now we apply our two-dimensional counterpart to the IVT:
Since y = 0 is contained yay! The area of mathematics which seeks to understand
continuity and connectedness • Far-reaching generalizations of theorems like our
“Two-dimensional Intermediate • Precise notions of what it means for a curve to “wrap n
times around • Generalizations of winding numbers for wrapping
higher-dimensional shapes • Knot theory. • Bottles whose insides and outsides are indistinguishable. . . . to name a few. It has been said that topologists
can’t tell their donuts from You might think, then, that algebraists would have a tough
time coping with Well, yes. People can be cruel. But this fact really just serves to illustrate that no
field of mathematics is entirely Consider the polynomial p(x) = x2 − 6x + 9. Then p(x)
factors as (x − 3)2, FUNDAMENTAL THEOREM OF ALGEBRA, strong form Theorem. Suppose p(x) is any polynomial of degree n > 0.
Then, if we Explanation: If p(x) has degree n > 0, the
regular-strength theorem shows Now, if n were 1, then p1(x) would have degree 0, and
hence be a constant. This Otherwise, p1(x) has degree ≥ 1, and the regular-strength
theorem applies again, Repeating this process exactly n times, we finally get to
the stage where pn(x) Double-yay! Here is another way we can interpret the Fundamental
Theorem of Algebra: The God created the natural numbers, and all the rest is the
work of In fact, we can think of the logical development of number
systems as a gradual • In the natural numbers, we can always add any pair of
numbers. But Z = {. . . − 3,−2,−1, 0, 1, 2, . . .}. • In the integers, we can always multiply, but only
sometimes divide. To
• But the rational numbers don’t include numbers like π
and
• And in R, equations like x2 = −1 still have no
solutions. So we introduce
The Fundamental Theorem of Algebra then says: We’re done. We now have as many solutions as we need to any sort of
polynomial equation So, as you can see, the algebraists really have nothing to
be ashamed of. But Hug an Algebraist Today! |


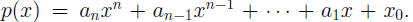 Then,
Then,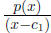 is another polynomial.
is another polynomial.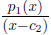 is another polynomial. Call it p2.
is another polynomial. Call it p2.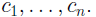
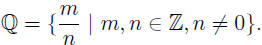
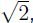 and also
and also