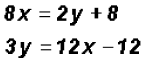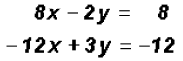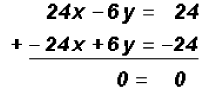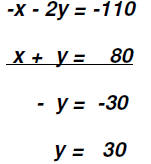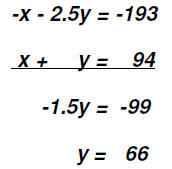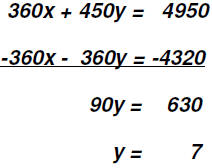|
Home Graphing and Writing Linear Functions SOLVING EQUATIONS INVOLVING RATIONAL EXPONENTS Linear Equations and Graphing Systems of Linear Equations Solving Polynomial Equations Matrix Equations and Solving Systems of Linear Equations Introduction Part II and Solving Equations Linear Algebra Graphing Linear Inequalities Using Augmented Matrices to Solve Systems of Linear Equations Solving Linear Inequalities Solution of the Equations Linear Equations Annotated Bibliography of Linear Algebra Books Write Linear Equations in Standard Form Graphing Linear Inequalities Introduction to Linear Algebra for Engineers Solving Quadratic Equations THE HISTORY OF SOLVING QUADRATIC EQUATIONS Systems of Linear Equations Review for First Order Differential Equations Systems of Nonlinear Equations & their solutions LINEAR LEAST SQUARES FIT MAPPING METHOD FOR INFORMATION RETRIEVAL FROM NATURAL LANGUAGE TEXTS Quadratic Equations Syllabus for Differential Equations and Linear Alg Linear Equations and Matrices Solving Linear Equations Slope-intercept form of the equation Linear Equations DETAILED SOLUTIONS AND CONCEPTS QUADRATIC EQUATIONS Linear Equation Problems Systems of Differential Equations Linear Algebra Syllabus Quadratic Equations and Problem Solving LinearEquations The Slope-Intercept Form of the Equation Final Exam for Matrices and Linear Equations Linear Equations |
Systems of Linear EquationsPLEASE NOTE THAT YOU CANNOT USE A CALCULATOR ON THE
ACCUPLACER - Systems of Linear Equations You already studied the linear equation in two variables
Ax + By = C whose graph is a Systems of Linear Equations can be solved graphically, or
by using the Substitution Method or the The following is a pictorial representation of the system
consisting of the linear equations
Solving a System of Linear Equations graphically often
does not give use the correct solution. For Actually, the solution is
Strategy for Solving Systems of Equations by the Substitution Method Step 1: Solve any one of the equations for one variable in
terms of the other. If one of Step 2: Substitute the expression found in Step 1 into the
other equation. You should Please note that ONLY at the point of intersection two
equations are equal to Step 3: To find the value of the second variable,
back-substitute the value of the variable Step 4: Form an ordered pair with the values found in Step
3 and Step 4. This is the Strategy for Solving Systems of Equations by the Addition Method Step 1: If necessary, rewrite both equations in the same
form so that the variables and Step 2: If necessary, multiply either equation or both
equations by appropriate numbers Step 3: Write the equations one below the other, draw a
horizontal line, then add each of Step 4: To find the value of the second variable,
back-substitute the value of the variable Step 5: Form an ordered pair with the values found in Step
4 and Step 5. This is the NOTE: Solving Systems of Linear Equations with the
Substitution Method is often quicker than Problem 1:
Let's use both the Substitution Method and the Addition Method. Substitution Method: Step 1: Solve any one of the equations for one variable in terms
of the other. By
Step 2:
Step 3:
Therefore, the solution to the linear system of
equations or the point of intersection Addition Method:
Step 1: The equations are already rewritten in the same form so
that the variables and Step 2:
Step 3:
The x-coordinate of the point of intersection. Step 4:
The solution to the system of linear equations or their
point of intersection is Problem 2:
We will use the Substitution Method because both variables
in the second equation have Solve the second equation for one variable in terms of the
other. It does not matter which By solving the equation
In this case, we can conclude that the System of Linear
Equations has NO solutions. This Problem 3:
We will use the Substitution Method because both equations
have variables with a In this case, both equations are already solved for y.
This is a perfect case for the
Solving for the y-coordinate using the equation
Therefore, the solution to the linear system of
equations or the point of intersection Problem 4:
We will use the Substitution Method because one variable
in the second equation has a Furthermore, the second equation is already solved for y. Back-substituting into the equation
Solving for the y-coordinate using the equation
Therefore, the solution to the linear system of
equations or the point of intersection Problem 5:
In this case, we will use the Addition Method because none
of the variables have a Let's eliminate x by multiplying the first equation by 3
and the second equation by -5.
To find the y-coordinate of the point of intersection of
the two lines, we back-substitute the
The solution to the system of linear equations or their
point of intersection is Problem 6:
First we must arrange the system so that the variable
terms appear on one side of the
Let's eliminate y by multiplying the first equation by 3
and the second equation by 2.
Since we not only eliminated y but also x, we have to
conclude that this System of Linear Problem 7: A grocer plans to mix candy that sells for $1.20 a pound
with candy that sells for $2.40 a Here we have enough information to make two equation in
two variables. Let's call the The first equation is an income equation: 1.20x + 2.40y =
1.65(80) 1.20x + 2.40y = 132 We'll divide the first equation by -1.20 and then use the Addition Method.
To find the value of x, we back-substitute the value found
for y into the equation x + y = x + 30 = 80 The grocer needs 50 lb of candy that sells for $1.20
and 30 lb of candy that sells for Problem 8: A charity has been receiving donations of dimes and
quarters. They have 94 coins in all. Here we again have enough information to make two equation
in two variables. Let's call The first equation is an income equation: 0.10x + 0.25y = 19.30 The second equation shows the total number of coins: x + y = 94 Therefore, we are solving the following system. 0.10x - 0.25y = 19.30 We'll divide the first equation by -0.10 and then use the Addition Method.
To find the value of x, we back-substitute the value found
for y into the equation x + y = x + 66 = 94 The charity has 28 dimes and 66 quarters. Problem 9: An apartment building contains 12 units consisting of one-
and two-bedroom apartments Here we again have enough information to make two equation
in two variables. Let's call The first equation is an income equation: 360x + 450y =
4950 360x + 450y = 4950 We'll multiply the second equation by -360 and then use the Addition Method.
To find the value of x, we back-substitute the value found
for y into the equation x + y = x + 7 = 12 The apartment building has 5 one-bedroom apartments and
7 two-bedroom |


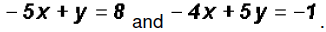 The point of intersection is considered the
solution of the
The point of intersection is considered the
solution of the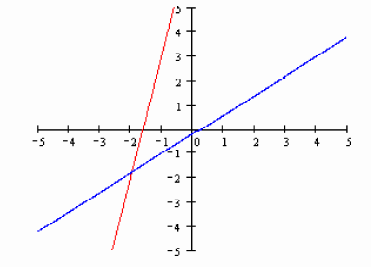
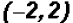 .
.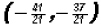 as you will see later, but this is difficult
to see on a graph.
as you will see later, but this is difficult
to see on a graph.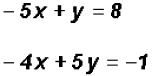
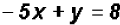 for y, we find
for y, we find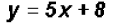
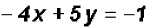 as follows
as follows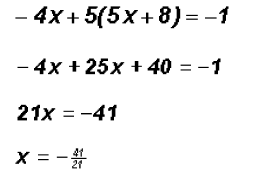
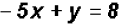 ,
we get
,
we get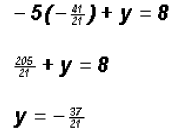
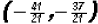 .
.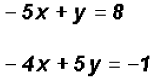
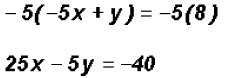
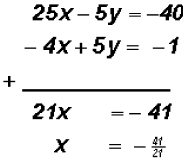
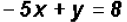 to
get
to
get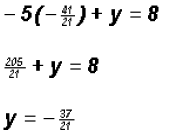
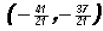 .
.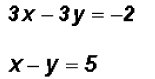
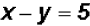 for x, we find
for x, we find 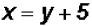 .
.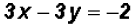 , we get
, we get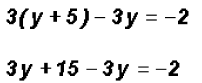
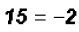 , which is, of course,
impossible.
, which is, of course,
impossible.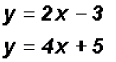
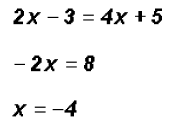
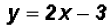 , we get
, we get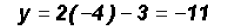
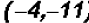 .
.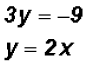
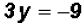 , we get
, we get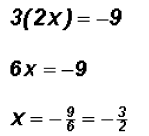
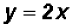 , we get
, we get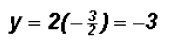
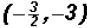 .
.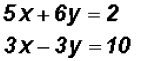
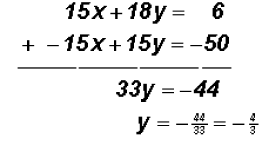
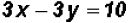 to get
to get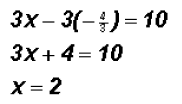
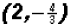 .
.