Quadratic Equations
Most text books provide a nice proof of the quadratic
formula. To derive the two
solutions for any quadratic equation we simply solve
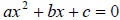 by completing the by completing the
square. This guide will focus on using the formula to solve problems.
Quadratic Formula: If
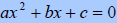 where a≠0 then where a≠0 then
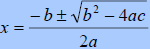 |
| |
Solve: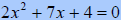 |
|
| Step 1: Identify a, b and c. |
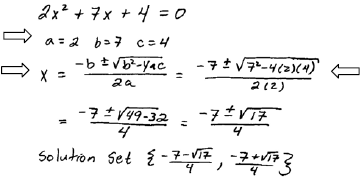 |
|
| Step 2: Write down the formula. |
Step 3: Plug in the
appropriate values and
evaluate. |
The argument of the square root
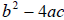 is called the discriminant and can be
used to is called the discriminant and can be
used to
determine the number and type of solutions to the quadratic equation without
doing all
the work to find the actual solutions.
Using the discriminant to determine the types
of solutions -
If 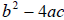 <0(negative) then there are two
nonreal complex solutions <0(negative) then there are two
nonreal complex solutions
If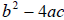 = 0(zero) then there is one real
solution = 0(zero) then there is one real
solution
If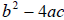 >0 If (positive) then there are two
real solutions >0 If (positive) then there are two
real solutions |
In the last problem 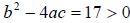 and we got two real solutions.
and we got two real solutions.
A. Use the Discriminant to determine the number and type of solutions.
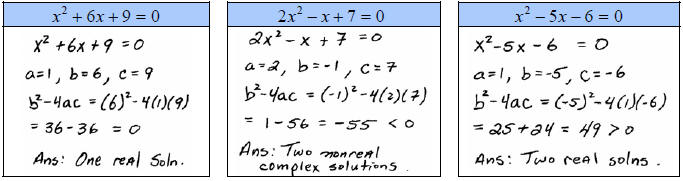
B. Solve using the quadratic formula.

If the discriminant is a perfect square then the quadratic
was factorable. In this case, it is
usually faster to solve by factoring and should be done that way unless stated
otherwise.
C. Solve using the quadratic formula.

|